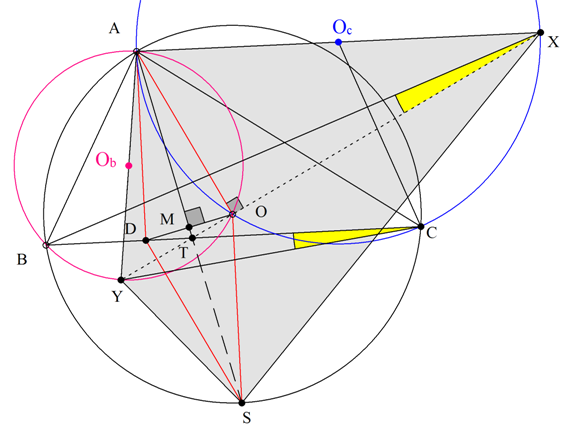
JBMO 2023 | Problem 4 - Solution - 26 June 2023

Problem 4.
Let ABC be an acute triangle with circumcenter O. Let D be the foot of the altitude from A to BC and let M be the midpoint of OD. The points O_b and O_c are the circumcenters of triangles AOC and AOB, respectively. If AO=AD, then prove that the points A, O_b, M and O_c are concyclic.

Solution
Let $X,Y$ be the reflections of $A$ across $O_c,O_b$ respectively, and $S$ be the midpoint of arc $BC$ in circle $(ABC)$ . Note that, $AD=AO=OS$ and $AD \parallel OS,$ hence quadrilateral $ADSO$ is a parallelogram, therefore points $A,M,S$ are collinear and so $M$ is the midpoint of $AS$ . We have the following Claim.

Claim: Quadrilateral $AXSY$ is cyclic.
Proof: Note that $\angle AOX=\angle AOY=90^\circ$ , and so $O \in XY$ . Moreover, if $XY$ intersects $BC$ at point $T$ , then $\angle AOT=\angle ADT=90^\circ$ , and since $AD=AO$ we obtain that $AT$ bisects $\angle DAO$ . Since $AD,AO$ are isogonal, this means $T \in AS$ .

To finish, note that

$\angle BXY=\angle BXO=180^\circ-\angle BAO=90^\circ+\angle C=\angle C+\angle ACY=\angle BCY,$

hence $BXCY$ is cyclic. Thus,

$TA \cdot TS=TB \cdot TC=TX \cdot TY,$

as desired $\blacksquare$

Back to the problem, since $AXSY$ is cyclic and $O_c,M,O_b$ are the midpoints of $AX,AS,AY$ respectively, we obtain that $AO_cMO_b$ is cyclic, too, as desired.